مجموعه های اعداد

اعداد طبیعی، اعدادی هستند که برای شمردن به کار می‌روند. مجموعه اعداد طبیعی {... ,۳ ,۲ ,۱} است.

در این مجموعه عدد صفر وجود ندارد و با اضافه کردن آن، مجموعه اعداد حسابی به وجود می‌آید. این مجموعه یک مجموعه نامتناهی است.

در ریاضیات، مجموعه اعداد طبیعی را با نماد N یا 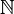نمایش می‌دهند. این حرف از آغاز واژه انگلیسی Natural، به معنای طبیعی، گرفته شده است.

اعداد حسابی همان اعداد طبیعی هستند که صفر هم به آنها اضافه شده است.

اعداد صحیح به مجموعه اعداد طبیعی مثبت و اعداد طبیعی منفی و عدد صفر گفته می‌شود. این مجموعه را در ریاضی معمولا با Z یا 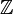(ابتدای کلمه zahlen که در زبان آلمانی به معنی اعداد است) نشان می‌دهند. مجموعه اعداد صحیح، مانند مجموعه اعداد طبیعی، یک مجموعه شمارای نامتناهی ست.

شاخه‌ای از ریاضیات که به مطالعه اعداد صحیح می پردازد، نظریه اعداد نام دارد.

اعداد گویا (یا به زبان دیگر، اعداد کسری) حاصل تقسیم دو عدد صحیح هستند، به شرطی که عدد دوم صفر نباشد. هر عدد گویا را به شکل a/b یا 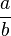می‌توان نوشت (که a و b اعداد صحیح اند).

در ریاضیات مجموعه اعداد گویا را با 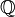نمایش می‌دهند. مجموعه اعداد گویا مجموعه‌ای شمارا است. این مجموعه، همچنین، زیرمجموعه‌ای چگال (dense) از مجموعهٔ اعداد حقیقی است.

اعداد گنگ، یا اعداد اصم، اعدادی حقیقی هستند که گویا نباشند، یعنی نتوان آن‌ها را به صورت کسری که صورت و مخرجش عدد صحیح باشند نوشت. مجموعه اعداد گنگ مجموعه‌ای ناشمارا است.

میدان تمام اعداد گویا و گنگ را اعداد حقیقی گویند و آن را با 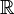نمایش میدهند. اعداد حقیقی را میتوان با اضافه کردن عدد موهومی(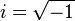) بسط داد. اعدادی به فرم a + bi که در آن a و b هر دو عدد حقیقی هستند را اعداد مختلط مینامند.

قانون جاذبه نیوتن

جاذبه یا به عبارت دقیقتر نیروی جاذبه نیرویی است که دو جسم را به طرف هم می‌کشد. این نیرو بین اجسام بزرگتر قویتر است. هر چه فاصله اجسام از هم بیشتر باشد، ضعیفتر عمل می‌کند. نیروی جاذبه زمین همه اشیاء سطح خود و یا نزدیک به سطح خود را به طرف مرکز خود می‌کشد. هرگاه یک توپ را به هوا پرتاب کنیم، توپ به زمین بر می‌گردد، این نیروی جاذبه است که آن را به طرف پایین می‌کشد و هر چه توپ را با نیروی بیشتری به هوا پرتاب کنیم، با همان نیرو به طرف زمین بر می‌گردد، و البته اگر بتوانیم با قدرت کافی آنرا پرتاب کنیم، می‌تواند از نیروی جاذبه زمین جدا شده و به فضا برود. برای بدست آوردن چنین نیرویی، به نیروی رانش موتور یک موشک نیاز داریم.

قانون نیوتن

فرضیه‌های اسحاق نیوتن در سال 1687 در کتابش با عنوان اصول ریاضی در فلسفه طبیعی منتشر شد. در این اثر ، او قانون عمومی جاذبه‌اش را اعلام کرد که در این جهان برای دو جرم کاربرد دارد. اسحاق نیوتن چنین محاسبه کرد که قدرت نیروی جاذبه میان 2 جسم به سه عامل بستگی دارد: جرم آن دو جسم و فاصله میان مراکزشان. با فرمولهای ریاضی ، این قانون چنین بیان می‌شود:

F = Gm₁m₂/r²

که F قدرت نیروی جاذبه ، m₂ ، m₁ دو جرم و r فاصله میان مراکز دو جرم و G عدد ثابت یا ثابت عمومی جاذبه است. قانون عمومی جاذبه نشان می‌دهد که هر چه جرم دو جسم بیشتر و فاصله‌شان کمتر باشد، آنها بیشتر به طرف یکدیگر کشیده می‌شوند. رابطه آنها تحت تأثیر قانون عکس مجذور قرار دارد، که بیان می‌کند کشش میان دو جسم با مجذور فاصله آنها کاهش می‌یابد. اگر زمین دو برابر مسافت فعلی از خورشید فاصله داشت، شدت نیروی جاذبه میان این دو جسم یک چهارم می‌شد. اگر زمین 5 برابر فاصله کنونی از خورشید دورتر بود، نیروی جاذبه 25 برابر کاهش می‌یافت.

پایداری و فرار در میدان جاذبه

این نیروی جاذبه زمین است که یک ماهواره را در مدار زمین نگه می‌دارد. سرعت لازم برای رفتن به مدار اطراف ماه 28000 کیلومتر در ساعت (17500 مایل در ساعت) است. خارج شدن از مدار زمین و به فضا رفتن نیازمند سرعت بیشتری است که آن را سرعت گریز از نیروی می‌نامند.سرعت گریز از نیروی جاذبه زمین 40320 کیلومتر در ساعت (25000 مایل در ساعت) است. چون نیروی جاذبه هر یک از سیارات و همچنین ماه با سیاره دیگر متفاوت است.

برای مثال ، سرعت گریز از جاذبه ماه یک پنجم سرعت گریز از جاذبه زمین است. کاوشگری که از نیروی جاذبه زمین فرار می‌کند، در مدار خورشید باقی می‌ماند و این بخاطر نیروی جاذبه خورشید است. این کاوشگر اگر بخواهد از منظومه شمسی خارج شود، باید سرعتی متناسب با سرعت گریز از جاذبه خورشید داشته باشد.